Cryptography: Theory and Practice by Douglas Stinson CRC Press, CRC Press LLC ISBN: 0849385210   Pub Date: 03/17/95

1.3 Notes

Much of the material on classical cryptography is covered in textbooks, for example Beker and Piper [BP82] and Denning [DE82]. The probability estimates for the 26 alphabetic characters are taken from Beker and Piper. As well, the cryptanalysis of the Vigenere Cipher is a modification of the description given in Beker and Piper.

A good reference for elementary number theory is Rosen [Ro93]. Background in elementary linear algebra can be found in Anton [AN91].

Kahn’s book “The Codebreakers” [KA67] is an entertaining and informative history of cryptography up to 1967. In it, Kahn states that the Vigenere Cipher is incorrectly attributed to Vigenere.

The Hill Cipher was first described in [HI29]. Much information on stream ciphers can be found in the book by Rueppel [RU86].

Exercises

1.1  Below are given four examples of ciphertext, one obtained from a Substitution Cipher, one from a Vigenere Cipher, one from an Affine Cipher, and one unspecified. In each case, the task is to determine the plaintext.

Give a clearly written description of the steps you followed to decrypt each ciphertext. This should include all statistical analysis and computations you performed.

The first two plaintexts were taken from “The Diary of Samuel Marchbanks,” by Robertson Davies, Clarke Irwin, 1947; the fourth was taken from “Lake Wobegon Days,” by Garrison Keillor, Viking Penguin, Inc., 1985.

(a)  Substitution Cipher:

      EMGLOSUDCGDNCUSWYSFHNSFCYKDPUMLWGYICOXYSIPJCK
      QPKUGKMGOLICGINCGACKSNISACYKZSCKXECJCKSHYSXCG
      OIDPKZCNKSHICGIWYGKKGKGOLDSILKGOIUSIGLEDSPWZU
      GFZCCNDGYYSFUSZCNXEOJNCGYEOWEUPXEZGACGNFGLKNS
      ACIGOIYCKXCJUCIUZCFZCCNDGYYSFEUEKUZCSOCFZCCNC
      IACZEJNCSHFZEJZEGMXCYHCJUMGKUCY

HINT  F decrypts to w.

(b)  Vigenere Cipher:

      KCCPKBGUFDPHQTYAVINRRTMVGRKDNBVFDETDGILTXRGUD
      DKOTFMBPVGEGLTGCKQRACQCWDNAWCRXIZAKFTLEWRPTYC
      QKYVXCHKFTPONCQQRHJVAJUWETMCMSPKQDYHJVDAHCTRL
      SVSKCGCZQQDZXGSFRLSWCWSJTBHAFSIASPRJAHKJRJUMV
      GKMITZHFPDISPZLVLGWTFPLKKEBDPGCEBSHCTJRWXBAFS
      PEZQNRWXCVYCGAONWDDKACKAWBBIKFTIOVKCGGHJVLNHI
      FFSQESVYCLACNVRWBBIREPBBVFEXOSCDYGZWPFDTKFQIY
      CWHJVLNHIQIBTKHJVNPIST

(c)  Affine Cipher:

      KQEREJEBCPPCJCRKIEACUZBKRVPKRBCIBQCARBJCVFCUP
      KRIOFKPACUZQEPBKRXPEIIEABDKPBCPFCDCCAFIEABDKP
      BCPFEQPKAZBKRHAIBKAPCCIBURCCDKDCCJCIDFUIXPAFF
      ERBICZDFKABICBBENEFCUPJCVKABPCYDCCDPKBCOCPERK
      IVKSCPICBRKIJPKABI

(d)  unspecified cipher:

      BNVSNSIHQCEELSSKKYERIFJKXUMBGYKAMQLJTYAVFBKVT
      DVBPVVRJYYLAOKYMPQSCGDLFSRLLPROYGESEBUUALRWXM
      MASAZLGLEDFJBZAVVPXWICGJXASCBYEHOSNMULKCEAHTQ
      OKMFLEBKFXLRRFDTZXCIWBJSICBGAWDVYDHAVFJXZIBKC
      GJIWEAHTTOEWTUHKRQVVRGZBXYIREMMASCSPBNLHJMBLR
      FFJELHWEYLWISTFVVYFJCMHYUYRUFSFMGESIGRLWALSWM
      NUHSIMYYITCCQPZSICEHBCCMZFEGVJYOCDEMMPGHVAAUM
      ELCMOEHVLTIPSUYILVGFLMVWDVYDBTHFRAYISYSGKVSUU
      HYHGGCKTMBLRX

1.2  

(a)  How many 2 × 2 matrices are there that are invertible over ?

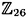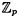(b)  Let p be prime. Show that the number of 2 × 2 matrices that are invertible over is (p² - 1)(p² - p).

HINT  Since p is prime, 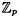is a field. Use the fact that a matrix over a field is invertible if and only if its rows are linearly independent vectors (i.e., there does not exist a non-zero linear combination of the rows whose sum is the vector of all 0′s).

(c)  For p prime, and m ≥ 2 an integer, find a formula for the number of m × m matrices that are invertible over .

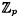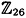1.3  Sometimes it is useful to choose a key such that the encryption operation is identical to the decryption operation. In the case of the Hill Cipher, we would be looking for matrices K such that K = K^-1 (such a matrix is called involutory). In fact, Hill recommended the use of involutory matrices as keys in his cipher. Determine the number of involutory matrices (over ) in the case m = 2.

HINT  Use the formula given in Theorem 1.3 and observe that det A = ±1 for an involutory matrix over .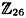

1.4  Suppose we are told that the plaintext

                            breathtaking

yields the ciphertext

                            RUPOTENTOSUP

where the Hill Cipher is used (but m is not specified). Determine the encryption matrix.

1.5  An Affine-Hill Cipher is the following modification of a Hill Cipher: Let m be a positive integer, and define . In this cryptosystem, a key K consists of a pair (L, b), where L is an m × m invertible matrix over 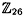, and 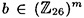. For x = (x₁, . . . , x_m) 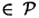and K = (L, b) 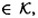, we compute y = e_K(x) = (y₁, . . . , y_m) by means of the formula y = xL + b. Hence, if 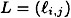and b = (b₁, . . . , b_m), then

Suppose Oscar has learned that the plaintext

                            adisplayedequation

is encrypted to give the ciphertext

                            DSRMSSIOPLXLJBZULLM

and Oscar also knows that m = 3. Compute the key, showing all computations.

1.6  Here is how we might cryptanalyze the Hill Cipher using a ciphertext-only attack. Suppose that we know that m = 2. Break the ciphertext into blocks of length two letters (digrams). Each such digram is the encryption of a plaintext digram using the unknown encryption matrix. Pick out the most frequent ciphertext digram and assume it is the encryption of a common digram in the list following Table 1.1 (for example, TH or ST). For each such guess, proceed as in the known-plaintext attack, until the correct encryption matrix is found.

Here is a sample of ciphertext for you to decrypt using this method:

        LMQETXYEAGTXCTUIEWNCTXLZEWUAISPZYVAPEWLMGQWYA
        XFTCJMSQCADAGTXLMDXNXSNPJQSYVAPRIQSMHNOCVAXFV

1.7  We describe a special case of a Permutation Cipher. Let m, n be positive integers. Write out the plaintext, by rows, in m × n rectangles. Then form the ciphertext by taking the columns of these rectangles. For example, if m = 4, n = 3, then we would encrypt the plaintext “cryptography” by forming the following rectangle:

                               cryp
                               togr
                               aphy

The ciphertext would be “CTAROPYGHPRY.”

(a)  Describe how Bob would decrypt a ciphertext (given values for m and n).

(b)  Decrypt the following ciphertext, which was obtained by using this method of encryption:

       MYAMRARUYIQTENCTORAHROYWDSOYEOUARRGDERNOGW

1.8  There are eight different linear recurrences over of degree four having c₀ = 1. Determine which of these recurrences give rise to a keystream of period 15 (given a non-zero initialization vector).

1.9  The purpose of this exercise is to prove the statement made in Section 1.2.5 that the m × m coefficient matrix is invertible. This is equivalent to saying that the rows of this matrix are linearly independent vectors over .

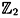As before, we suppose that the recurrence has the form

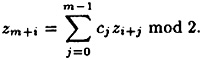
(z₁, . . . , z_m) comprises the initialization vector. For i ≥ 1, define

Note that the coefficient matrix has the vectors v₁, . . . , v_m as its rows, so our objective is to prove that these m vectors are linearly independent.

Prove the following assertions:

(a)  For any i ≥ 1,

(b)  Choose h to be the minimum integer such that there exists a non-trivial linear combination of the vectors v₁, . . . , v_h which sums to the vector (0, . . . , 0) modulo 2. Then

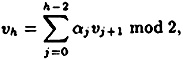
and not all the αj′s are zero. Observe that h ≤ m + 1, since any m + 1 vectors in an m-dimensional vector space are dependent.

(c)  Prove that the keystream must satisfy the recurrence

for any i ≥ 1.

(d)  Observe that if h ≤ m, then the keystream satisfies a linear recurrence of degree less than m, a contradiction. Hence, h = m + 1, and the matrix must be invertible.

1.10  Decrypt the following ciphertext, obtained from the Autokey Cipher, by using exhaustive key search:

                       MALVVMAFBHBUQPTSOXALTGVWWRG

1.11  We describe a stream cipher that is a modification of the Vigenere Cipher. Given a keyword (K₁, . . . , K_m) of length m, construct a keystream by the rule z_i = K_i (1 ≤ i ≤ m), z_i + m = z_i + 1 mod 26 (i ≥ m + 1). In other words, each time we use the keyword, we replace each letter by its successor modulo 26. For example, if SUMMER is the keyword, we use SUMMER to encrypt the first six letters, we use TVNNFS for the next six letters, and so on.

Describe how you can use the concept of index of coincidence to first determine the length of the keyword, and then actually find the keyword.

Test your method by cryptanalyzing the following ciphertext:

          IYMYSILONRFNCQXQJEDSHBUIBCJUZBOLFQYSCHATPEQGQ
          JEJNGNXZWHHGWFSUKULJQACZKKJOAAHGKEMTAFGMKVRDO
          PXNEHEKZNKFSKIFRQVHHOVXINPHMRTJPYWQGJWPUUVKFP
          OAWPMRKKQZWLQDYAZDRMLPBJKJOBWIWPSEPVVQMBCRYVC
          RUZAAOUMBCHDAGDIEMSZFZHALIGKEMJJFPCIWKRMLMPIN
          AYOFIREAOLDTHITDVRMSE

The plaintext was taken from “The Codebreakers,” by D. Kahn, Macmillan, 1967.